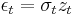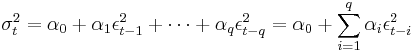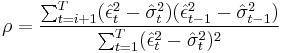Autoregressive conditional heteroskedasticity
In econometrics, AutoRegressive Conditional Heteroskedasticity (ARCH) models are used to characterize and model observed time series. They are used whenever there is reason to believe that, at any point in a series, the terms will have a characteristic size, or variance. In particular ARCH models assume the variance of the current error term or innovation to be a function of the actual sizes of the previous time periods' error terms: often the variance is related to the squares of the previous innovations.
Such models are often called ARCH models (Engle, 1982), although a variety of other acronyms are applied to particular structures of model which have a similar basis. ARCH models are employed commonly in modeling financial time series that exhibit time-varying volatility clustering, i.e. periods of swings followed by periods of relative calm.
Contents |
ARCH(q) model Specification
Suppose one wishes to model a time series using an ARCH process. Let 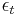 denote the error terms (return residuals, with respect to a mean process) i.e. the series terms. These
denote the error terms (return residuals, with respect to a mean process) i.e. the series terms. These 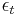 are split into a stochastic piece
are split into a stochastic piece 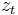 and a time-dependent standard deviation
and a time-dependent standard deviation 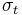 characterizing the typical size of the terms so that
characterizing the typical size of the terms so that
where 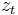 is a random variable drawn from a Gaussian distribution centered at 0 with standard deviation equal to 1. (i.e.
is a random variable drawn from a Gaussian distribution centered at 0 with standard deviation equal to 1. (i.e. 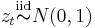 ) and where the series
) and where the series  are modeled by
are modeled by
and where 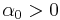 and
and 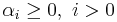 .
.
An ARCH(q) model can be estimated using ordinary least squares. A methodology to test for the lag length of ARCH errors using the Lagrange multiplier test was proposed by Engle (1982). This procedure is as follows:
- Estimate the best fitting autoregressive model AR(q)
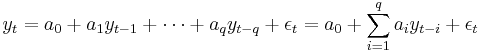 .
. - Obtain the squares of the error
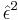 and regress them on a constant and q lagged values:
and regress them on a constant and q lagged values:
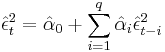
- where q is the length of ARCH lags.
- The null hypothesis is that, in the absence of ARCH components, we have
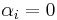 for all
for all 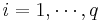 . The alternative hypothesis is that, in the presence of ARCH components, at least one of the estimated
. The alternative hypothesis is that, in the presence of ARCH components, at least one of the estimated 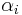 coefficients must be significant. In a sample of T residuals under the null hypothesis of no ARCH errors, the test statistic TR² follows
coefficients must be significant. In a sample of T residuals under the null hypothesis of no ARCH errors, the test statistic TR² follows 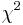 distribution with q degrees of freedom. If TR² is greater than the Chi-square table value, we reject the null hypothesis and conclude there is an ARCH effect in the ARMA model. If TR² is smaller than the Chi-square table value, we do not reject the null hypothesis.
distribution with q degrees of freedom. If TR² is greater than the Chi-square table value, we reject the null hypothesis and conclude there is an ARCH effect in the ARMA model. If TR² is smaller than the Chi-square table value, we do not reject the null hypothesis.
GARCH
If an autoregressive moving average model (ARMA model) is assumed for the error variance, the model is a generalized autoregressive conditional heteroskedasticity (GARCH, Bollerslev(1986)) model.
In that case, the GARCH(p, q) model (where p is the order of the GARCH terms 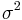 and q is the order of the ARCH terms
and q is the order of the ARCH terms 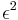 ) is given by
) is given by
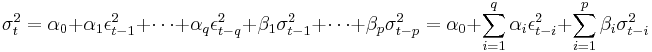
Generally, when testing for heteroskedasticity in econometric models, the best test is the White test. However, when dealing with time series data, this means to test for ARCH errors (as described above) and GARCH errors (below).
Prior to GARCH there was EWMA which has now been superseded by GARCH, although some people utilise both.
GARCH(p, q) model specification
The lag length p of a GARCH(p, q) process is established in three steps:
- Estimate the best fitting AR(q) model
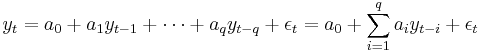 .
.
- Compute and plot the autocorrelations of
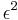 by
by
- The asymptotic, that is for large samples, standard deviation of
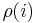 is
is 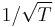 . Individual values that are larger than this indicate GARCH errors. To estimate the total number of lags, use the Ljung-Box test until the value of these are less than, say, 10% significant. The Ljung-Box Q-statistic follows
. Individual values that are larger than this indicate GARCH errors. To estimate the total number of lags, use the Ljung-Box test until the value of these are less than, say, 10% significant. The Ljung-Box Q-statistic follows 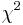 distribution with n degrees of freedom if the squared residuals
distribution with n degrees of freedom if the squared residuals 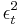 are uncorrelated. It is recommended to consider up to T/4 values of n. The null hypothesis states that there are no ARCH or GARCH errors. Rejecting the null thus means that there are existing such errors in the conditional variance.
are uncorrelated. It is recommended to consider up to T/4 values of n. The null hypothesis states that there are no ARCH or GARCH errors. Rejecting the null thus means that there are existing such errors in the conditional variance.
NGARCH
Nonlinear GARCH (NGARCH) also known as Nonlinear Asymmetric GARCH(1,1) (NAGARCH) was introduced by Engle and Ng in 1993.

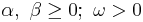 .
.
For stock returns, parameter 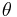 is usually estimated to be positive; in this case, it reflects the leverage effect, signifying that negative returns increase future volatility by a larger amount than positive returns of the same magnitude.[1][2]
is usually estimated to be positive; in this case, it reflects the leverage effect, signifying that negative returns increase future volatility by a larger amount than positive returns of the same magnitude.[1][2]
This model shouldn't be confused with the NARCH model, together with the NGARCH extension, introduced by Higgins and Bera in 1992.
IGARCH
Integrated Generalized Autoregressive Conditional Heteroskedasticity IGARCH is a restricted version of the GARCH model, where the persistent parameters sum up to one, and therefore there is a unit root in the GARCH process. The condition for this is
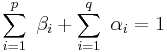 .
.
EGARCH
The exponential general autoregressive conditional heteroskedastic (EGARCH) model by Nelson (1991) is another form of the GARCH model. Formally, an EGARCH(p,q):
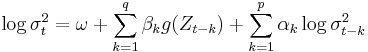
where 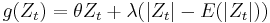 ,
, 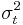 is the conditional variance,
is the conditional variance,  ,
,  ,
,  ,
,  and
and  are coefficients, and
are coefficients, and 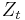 may be a standard normal variable or come from a generalized error distribution. The formulation for
may be a standard normal variable or come from a generalized error distribution. The formulation for 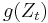 allows the sign and the magnitude of
allows the sign and the magnitude of 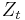 to have separate effects on the volatility. This is particularly useful in an asset pricing context.[3]
to have separate effects on the volatility. This is particularly useful in an asset pricing context.[3]
Since 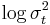 may be negative there are no (fewer) restrictions on the parameters.
may be negative there are no (fewer) restrictions on the parameters.
GARCH-M
The GARCH-in-mean (GARCH-M) model adds a heteroskedasticity term into the mean equation. It has the specification:
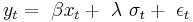
The residual 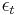 is defined as
is defined as
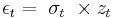
QGARCH
The Quadratic GARCH (QGARCH) model by Sentana (1995) is used to model symmetric effects of positive and negative shocks.
In the example of a GARCH(1,1) model, the residual process 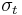 is
is
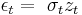
where 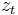 is i.i.d. and
is i.i.d. and
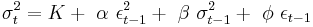
GJR-GARCH
Similar to QGARCH, The Glosten-Jagannathan-Runkle GARCH (GJR-GARCH) model by Glosten, Jagannathan and Runkle (1993) also models asymmetry in the ARCH process. The suggestion is to model 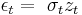 where
where 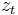 is i.i.d., and
is i.i.d., and
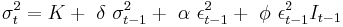
where 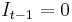 if
if 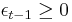 , and
, and 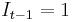 if
if 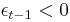 .
.
TGARCH model
The Threshold GARCH (TGARCH) model by Zakoian (1994) is similar to GJR GARCH, and the specification is one on conditional standard deviation instead of conditional variance:
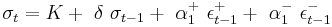
where 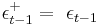 if
if 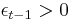 , and
, and 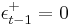 if
if 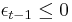 . Likewise,
. Likewise, 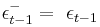 if
if 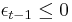 , and
, and 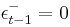 if
if 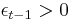 .
.
fGARCH
Hentschel's fGARCH model,[4] also known as Family GARCH, is an omnibus model that nests a variety of other popular symmetric and asymmetric GARCH models including APARCH, GJR, AVGARCH, NGARCH, etc.
References
- ^ Engle, R.F.; Ng, V.K. (1991). "Measuring and testing the impact of news on volatility". Journal of Finance 48 (5): 1749–1778. http://papers.ssrn.com/sol3/papers.cfm?abstract_id=262096.
- ^ Posedel, Petra (2006). "Analysis Of The Exchange Rate And Pricing Foreign Currency Options On The Croatian Market: The Ngarch Model As An Alternative To The Black Scholes Model". Financial Theory and Practice 30 (4): 347–368. http://www.ijf.hr/eng/FTP/2006/4/posedel.pdf.
- ^ St. Pierre, Eilleen F (1998): Estimating EGARCH-M Models: Science or Art, The Quarterly Review of Economics and Finance, Vol. 38, No. 2, pp. 167-180 [1]
- ^ Hentschel, Ludger (1995). All in the family Nesting symmetric and asymmetric GARCH models, Journal of Financial Economics, Volume 39, Issue 1, Pages 71-104
- Bollerslev, Tim (1986). "Generalized Autoregressive Conditional Heteroskedasticity", Journal of Econometrics, 31:307-327
- Bollerslev, Tim (2008). Glossary to ARCH (GARCH), working paper
- Enders, W. (1995). Applied Econometrics Time Series, John-Wiley & Sons, 139-149, ISBN 0471111635
- Engle, Robert F. (1982). "Autoregressive Conditional Heteroscedasticity with Estimates of Variance of United Kingdom Inflation", Econometrica 50:987-1008. (the paper which sparked the general interest in ARCH models)
- Engle, Robert F. (2001). "GARCH 101: The Use of ARCH/GARCH Models in Applied Econometrics", Journal of Economic Perspectives 15(4):157-168. (a short, readable introduction) Preprint
- Engle, R.F. (1995) ARCH: selected readings. Oxford University Press. ISBN 0-19-877432-X
- Gujarati, D. N. (2003) Basic Econometrics, 856-862
- Hacker, R. S. and Hatemi-J, A. (2005). A Test for Multivariate ARCH Effects, Applied Economics Letters, 12(7), 411–417.
- Nelson, D. B. (1991). "Conditional heteroskedasticity in asset returns: A new approach", Econometrica 59: 347-370.
|
||||||||